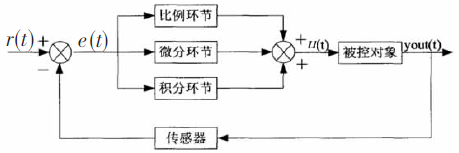
具有百余年历史的著名 “比例-积分-微分（PID）” 控制器，由于其结构简单、不依赖被控对象具体数学模型、且鲁棒性强等突出优点，是迄今为止实际工程技术系统中应用最为广泛的控制器，例如，95%以上的过程控制迴路都是基于PID控制。此外，PID控制器的影响已经远远超出自动控制领域自身，涉及到科学技术领域中各种各样需要进行反馈调控的系统或对象。然而，长期以来在实际应用中，PID控制器中三个关键参数的选择，一直都是基于局部线性化的模型，或主要依赖设计者的个人经验或实验。因此，对于真正的非线性不确定性实际被控对象，近百年来在控制理论上一直缺乏严格的稳定性保证，也没有关于PID参数设计的具体理论指导。这是长期以来国际控制界没有解决的重大科学问题。最近，郭雷院士与其研究生赵成所完成的这项科研成果，针对由牛顿第二定律所描述的一般二阶非线性不确定系统，首次定量地给出了使得闭环系统全局稳定时，PID控制器参数应当属于的三维无界开流形；并且针对一类自治非线性不确定系统，从数学上严格证明为了使闭环系统全局稳定，PID控制器参数所应满足的充分必要条件，从而建立了PID控制器的理论基础并给出了参数的设计方法。这一理论严格说明了PID控制器无论对非线性系统的不确定性结构，还是对PID 控制器的三个参数选择，都具有大范围的鲁棒性。这一理论和方法不仅为工程技术中广泛应用的PID控制器提供了理论基础、阐明了其被广泛应用的根本科学原理，而且还将为改进现有实际工程控制系统的性能以及设计新型控制系统，提供必要的理论基础和可靠的设计指导。这是控制理论研究的一项重大突破。美国加州大学圣迭戈分校教授Miroslav Krstic (IEEE Fellow, IFAC Fellow, SIAM Fellow)发表在2017年National Science Review上的文章评价该工作：“a highly valuable paper for both the control practitioner and for the theorist”。相关成果发表在2017年第 2 期《中国科学：信息科学》 (Science China, Information Sciences, [60(2), 1-13, 2017])上。 

  Towards a mathematical theory of PID control 

　　It is well-known that, despite of the remarkable progresses in modern control theory over the past half a century, the classical PID (proportional-integral- derivative) controller is still the most widely used ones in engineering systems by far. The PID controller is simply a weighted linear combination of the proportional, integral and derivative terms of the system regulation errors to be controlled, where the three weights are called the PID parameters whose design does not need precise mathematical models of the systems to be controlled. However, in engineering practice, the PID parameters are traditionally chosen based on experiment or experiences or by both, there is lack of a theoretical method on the choice of PID parameters and a theoretical analysis on the performance of PID controllers for practical nonlinear uncertain dynamical systems. A latest research gives a simple and analytic design method for the PID parameters for second order nonlinear uncertain systems, and establishes a mathematical theory for global stability and asymptotic regulation of the closed-loop control systems, which is of high value for both PID control theory and its wide practice.  

　　代表性论文： 

　　Cheng Zhao and Lei Guo, PID controller design for second order nonlinear uncertain systems, Science China, Information Sciences, 60(2), 1-13, 2017.